Automatische Tubular Bells (1 / 6 stap)

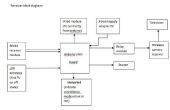
Stap 1: Bouw van de buisklokken

Eerste stap was het vinden van een goede en goedkope materiaal te bouwen chimes. Na sommige winkels bezoekt en doen sommige tests, vond ik dat aluminium is het materiaal die gaf me de beste geluidskwaliteit vs. prijs relatie. Dus kocht ik 6 bars van 1 meter lengte van elkaar. Ze hadden een 1, 6cm buitendiameter en 1,5 cm-binnendiameter (1mm dikte) eens had ik de balken die ik snijden ze op de goede lengte moest om de frequentie van elke noot. Ik zocht op internet en vond enkele interessante sites die mij veel interessante informatie over het berekenen van de lengte van elke balk om de frequenties die ik wilde (zie links sectie). Onnodig te zeggen was dat de frecuency ik was op zoek naar de fundamentele frecuency van elke noot en als gebeurt in bijna alle instrumenten, de bars zal produceren andere simultaneos frecuencies appart van de grondrechten. Dit andere gelijktijdige frecuenices worden de harmonischen die normaliter veelvoud van de fundamentele frecuency. Het aantal, de duur en de verhouding van deze harmonischen is het verantwoordelijk voor insturment de klankkleur.

De relatie tussen de frequentie van een noot en de zelfde nota in het volgende octaaf is 2. Dus als de fundamentele frequentie van C notitie 261.6Hz, de fundamentele frequentie van C in het volgende octaaf 2 zullen * 261.6 = 523, 25 Hz. Zoals we weten dat de westerse Europese muziek verdeelt een octaaf in 12 stappen van schaal (12 halve tonen ingedeeld in 7 notities en 5 duurzame notities), kunnen we de frequentie van de volgende halve Toon berekenen door te vermenigvuldigen met 2 # vorige opmerking frequentie (1/12). Zoals we weten dat C frequentie 261.6Hz is en de verhouding tussen 2 conescutive halve tonen 2 is # kunnen (1/12) we alle notities frecuencies afleiden:

Opmerking: het # symbool vertegenwoordigt de exploitant van de macht. Bijvoorbeeld: "een # 2" is hetzelfde dat "een^2"

Opmerking Freq
01 C 261.6 Hz
02 Csust 261.6 * (2 # (1/12)) = 277.18 Hz
03 D 277.18 * (2 # (1/12)) = 293,66 Hz
04 Dsust 293,66 * (2 # (1/12)) = 311,12 Hz
05 E 311,12 * (2 # (1/12)) = 329.62Hz
06-F 329,62 * (2 # (1/12)) = 349.22 Hz
07 Fsust 349.22 * (2 # (1/12)) = 369.99 Hz
08 G 369.99 * (2 # (1/12)) = 391.99 Hz
09 Gsust 391.99 * (2 # (1/12)) = 415.30 Hz
10 een 415.30 * (2 # (1/12)) = 440.00 Hz
11 Asust 440,00 * (2 # (1/12)) = 466,16 Hz
12 B 466,16 * (2 # (1/12)) = 493.88 Hz
13 C 493.88 * (2 # (1/12)) = 2 * 261.6 = 523.25 Hz

Bovenstaande tabel is slechts voor informatie-doel en het is niet nodig voor het berekenen van de lengte van de balken. Het belangrijkste ding is de factor van de relatie tussen de frequenties: 2 voor de zelfde nota in het volgende octaaf, en (2 # (1/12) voor de volgende halve toon. We zullen het gebruiken in de formule gebruikt voor het berekenen van de lengte van de balken. De oorspronkelijke formule die ik vond op Internet (zie links sectie) is:

F1/f2 = (L2/L1) # 2

Hieruit kunnen we gemakkelijk afleiden de formule die laat ons berekenen van de lengte van elke balk. F2 is de frecuency van de volgende noot die we willen berekenen en we willen weten volgende halve Toon frequentie: f2 = f1 * (2 # (1/12))

F1/(F1*(2#(1/12))) =(L2/L1) #2
...
L1*(1/(2#(1/24))) = L2

de formule is:

L2=L1*(2#(-1/24))

Dus met deze formule kunnen we afleiden de lengte van de Gong die volgende halve Toon spelen zal, maar uiteraard zullen we de lengte van de Gong die de eerste noot speelt. Hoe kunnen we het berekenen? Ik weet niet hoe te berekenen van de lengte van de eerste Gong. Ik veronderstellen dat bestaat een formule die betrekking heeft op de fysieke eigenschappen van het materiaal, de grootte van de balk (lengte, uiterlijke en innerlijke diameter) met de frequentie zal spelen, maar ik weet het niet. Ik vond het gewoon door het af te stemmen met de hulp van mijn oor en gitaar (u kunt ook een stemvork of een PC geluidskaart frecuencemeter om het af te stemmen).