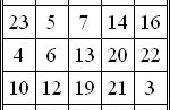
Stap 1: De symmetrische magisch vierkant

Er zijn vele manieren van de bouw van een magische sqaure, maar ik zal u slechts tonen mijne.
Voorwaarden: De 2D matrix moet groter zijn dan 3 en altijd vreemd in grootte.
De functie:
f(y) = 2 * x mod grootte
OR
Voor x = 0 tot grootte-1
Matrix ((OffsetX + x) mod grootte, (OffsetY + 2 * x) mod grootte) = Nr
volgende
Nu wij het hebben van een magisch vierkant, maar is niet symmetrisch of concentrische, zodat we de matrix 180 graden draaien en hen bij elkaar optelt.
Voor x = 0 tot en met maat - 1
Voor y = 0 tot en met maat - 1
Matrix(x,y) = Matrix(x,y) + Matrix (grootte - x - 1, grootte - y - 1)
Volgende
Volgende
Dan zijn we een mirror van de oorspronkelijke matrix en toe te voegen aan het bovenstaande bij elkaar opgeteld.
Voor x = 0 tot en met maat - 1
Voor y = 0 tot en met maat - 1
Matrix(x,y) = Matrix(x,y) + Matrix (grootte - x - 1, y)
Volgende
Volgende
Het resultaat is een symmetrische magisch vierkant.
U kunt het uitvoeren van een nieuwe f(y) = 2 x * mod grootte bovenop de oude matrix en vervolgens herhalen de 180 graden en spiegel bediening voor eeuwig.
Matrix van dezelfde grootte met dezelfde operaties toegepast kunnen worden toegevoegd of aftrekken van elkaars. Vermenigvuldigen of gedeeld met een constante en zal nog steeds worden symmetrisch magische vierkanten.
Download mijn Visual Basic 2010 programma en source code te spelen.