Stap 1: Tellen in decimale notatie

Om te begrijpen in binaire tellen, is het het beste om te begrijpen hoe decimale werkt.
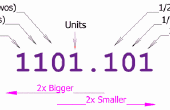
Voor elk nummer verwijst elke cijfer naar een positie.
In het nummer 576. Het cijfer 6 is op positie 0 en het cijfer 7 is op positie 1, het cijfer 5 bevindt zich op positie 3. Deze posities beginnen bij nul, met één voor elk cijfer dat in het getal te verhogen.
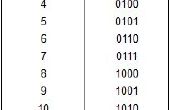
Decimale getallen worden ook wel grondtal 10, omdat de waarde van elk cijfer is gebaseerd op het nummer 10. Base 10 vertegenwoordigt ook het bedrag van de cijfers die in een cijfer resulteert. In basis 10 zijn er 10 cijfers die in een getal resulteert. Dit zijn 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Terugkijken op het nummer 576 zien precies hoe dit werkt begint met het cijfer '6'. Het visuele hulpmiddel is toegevoegd in deze stap te geven een grondig overzicht van elke stap in het volgende voorbeeld. Het visuele hulpmiddel en volgende voorbeeld gebruik hetzelfde proces.
Voorbeeld
Aangezien grondtal 10 wordt gebruikt bij het tellen in decimale notatie, en 6 gebeurt op positie 0. Wij nemen het cijfer vermenigvuldigd met 10 tot de macht van 0. Omdat iets tot de macht van 0 1, ons antwoord uitziet: 6 x 1 = 6.
Voor het cijfer 7 hebben we 7 vermenigvuldigd met 10 tot de macht van 1. Dit ziet er als volgt: 7 x 10 = 70.
Tot slot, voor het cijfer 5 hebben we 5 meerdere door 10 tot de macht van 2. Dit ziet eruit als 5 x 100 = 500.
Nadat u de waarde voor elk cijfer op hun respectieve standpunten ontdekt heb, kloppen alle van onze resultaten voor het definitieve antwoord. Dit ziet er als volgt: 6 + 70 + 500 = 576, die het oorspronkelijke getal is.
Nu uiteraard hoefde je niet te gaan door alle extra stappen voor dit nummer. Dit is altijd het geval is met grondtal 10, want dit de universele manier is om getallen tellen. Als er nummers in binaire, is het niet altijd duidelijk wat deze getallen gelijk aan.