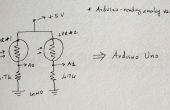
Stap 4: Experimenteren: Sample Rate



De simulator als set hier uitgangen altijd een mooi glad sinusgolf van amplitude 1. Voor het eerste experiment zullen we knoeien met de samplefrequentie, als aangepast door delta_t, het tijdsverschil tussen de monsters. We moeten geen ruis of andere verwerking. De code maakt gebruik van 3 bemonsteringsfrequenties (delta_t = 1,0, 0,1 en 0,01.) Aangezien de grafieken boven op elkaar vallen produceert het experiment 3 verschillende grafieken. De resulterende grafieken zijn de beelden voor deze stap.
def experiment_with_sample_rates( self ): print """ Experiment with Sample Rates Looking at different sample rates by changing delta T """ self.start_plot( plot_title = "Experiment Sample Rates 1/3: Delta T = 1.0") self.add_sensor_data( name = "dt = 1.", amplitude = 1., noise_amp = .0, delta_t = 1., max_t = 10., run_ave = 0, trigger_value = 0 ) self.show_plot( ) # ------------------------------------------------ self.start_plot( plot_title = "Experiment Sample Rates 2/3: Delta T = 0.1") self.add_sensor_data( name = "dt = 1.", amplitude = 1., noise_amp = .0, delta_t = 0.1, max_t = 10., run_ave = 0, trigger_value = 0 ) self.show_plot( ) # ------------------------------------------------ self.start_plot( plot_title = "Experiment Sample Rates 3/3: Delta T = 0.01") self.add_sensor_data( name = "dt = 1.", amplitude = 1., noise_amp = .0, delta_t = 0.01, max_t = 10., run_ave = 0, trigger_value = 0 ) self.show_plot( )
Om uit te voeren het gebruik van de lijn: sim_logging.experiment_with_sample_rates()
Mogelijke conclusies:
- Te laag een sampling-frequentie is echt slecht.
- Hoge tarieven zijn beter.