Vorig jaar raakte ik geïnteresseerd in voronoi patronen. Deze patronen zijn te vinden in de natuur (ex., zeepbellen, vlinder vleugels, giraffe vlekken, enz.). Bovendien, worden deze patronen toegepast in de economie, wiskunde en rekenkundige meetkunde ook. Ze zijn een "Voronoi-Diagram" genoemd. Andere Machine-Co. heeft een grote definitie voor Voronoi-Diagram:
Een Voronoi-diagram is een wiskundige methode ruimte verdelen in regio's. Zaad vlekken zijn verspreid langs een veld, en polygonen worden gegenereerd rond deze zaad-vlekken. De polygonen zijn elk punt in de ruimte rondom een zaad ter plaatse dat dichter bij dat zaad plek dan elke andere (hier is een beetje meer over hen als je nieuwsgierig bent).
Als een computationele ontwerper, ben ik voortdurend op zoek naar nieuwe algoritmen om te helpen nieuwe en nieuwe formulieren maken. Na veel onderzoek op voronoi patronen begon ik te schetsen met code (openFrameworks).
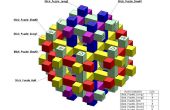
Ik heb vervolgens een applicatie die stond me toe om te analyseren van de cel sites van het voronoi-diagram en om te begrijpen hoe deze 2D diagrammen doorheen de tijd evolueren. De toepassing ook stond me toe om te zien de 3D vormen gemaakt door de segmenten van de 2D cel gestapeld na verloop van tijd. U kunt zien dat sommige van wat ik bedoel in de video hierboven; Merk op hoe de 3D vormen evolueren in de tijd als de cel sites verplaatsen.
Individueel, zijn deze 3D-vormen niet van deze wereld. Ze maken een uitdagende, maar leuke, puzzel samen te stellen. Ik uitgebreid de toepassing om 3D print de puzzel. In dit Instructable, ik zal worden met een beschrijving van hoe te genereren en afdrukken van de puzzel hierboven.