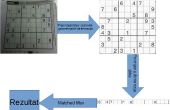
Stap 1: Visualisatie *

Kijk voor afzonderlijke cellen binnen de blokken die een horizontale of verticale lijnen die kunnen worden getrokken uit een van de nummers op het bord, dan plaatst u dat nummer wanneer u hen vinden elkaar niet overlappen. Een eenvoudiger manier om te denken dit is vinden alle van de 1 op het bord, tekent u lijnen voor geestelijke verticaal en horizontaal korting op alle van hen, dan zien als vindt u alle blokken waar al maar één cel is hetzij de overschrijding van deze lijnen of door andere grote aantallen gevuld. Wanneer je dat doet, zou je weten dat u die cel met een 1 invullen kunt; Dit kan worden gedaan met een willekeurig getal.
In mijn voorbeeld gegeven trok ik de lijnen af van elk 8 op het bord en in de bovenste rechts blok er is één cel die doet niet over een van hen, zo dat blok moet een 8. Verzorgen niet in te vullen het midden 2 blokken echter, beiden hebben al een 8 en de puzzel op dat punt zou verkeerd zijn.
De logica achter deze stap is dat om voor elke rij, kolom en blok hebben de nummers 1-9, absoluut geen rij, kolom of blok hetzelfde nummer twee keer kunt houden, dus visualiseren lijnen af van elk één exemplaar van een nummer, u effectief blijkt zelf alle plaatsen een nummer kan niet gaan.