Het vinden van het Volume van een Object met behulp van integratie (5 / 11 stap)

Stap 5: Shell methode

Nu dat we hoe weten te integreren, we gonna een methode die bekend staat als de Shell-methode gebruiken. De naam Shell methode komt van het feit dat je elk moment in een grafiek kiezen kunt, dat punt rond de y-as draaien, en het moet nemen op het uiterlijk van een schelp. Door de integratie van deze rotatie, kunt u het volume van de functie als het waren rond de y-as gedraaid.

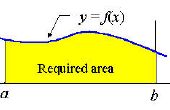
Wees ervan bewust dat integratie de volume onder de curve, vindt terwijl we eigenlijk willen vinden van het volume boven de curve.

De methode van de Shell is gevonden door de integratie van de straal van een object door de hoogte. De straal van een object vertegenwoordigt welk punt u te op elk punt op de grafiek halen. De straal is meestal gewoon gelijk is aan x. De hoogte is hoe hoog de functie is op elk punt op de grafiek.

Na integreren, vermenigvuldigt u het aantal door 2π. Dit geeft ons het volume van de functie tussen x = 0 en x = 2 rond de y-as gedraaid. De formule is hierboven weergegeven.