Stap 1: Functioneel Complete Set

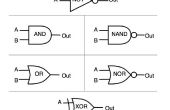
Er zijn een heleboel logica poorten met unieke reactie op logica ingangen. Voor nu laat focus op logica poorten met één tot twee logica ingangen namelijk: niet, AND, OR, NAND, noch, XOR, XNOR en vele anderen. Als wij uitvoeren elke één van hen willen, zou duren veel tijd aan het ontwerpen van een circuit. Uitvoering van een aantal van de poorten wellicht een heleboel transistoren in het werkelijke circuit. Nou, hou ik niet van die.
Tegen die tijd moeten we beseffen dat sommige logic-poorten kunnen worden gevormd door een combinatie van twee of meer logic-poorten. Dit rekening houdend met, besloot ik om het ontwerp van een circuit alleen voor één of twee logic-poorten die een functioneel complete set vormen zou. Deze set zou uitstrekken over alle andere logica poorten en elke logische poort kan worden uitgevoerd door een combinatie van de elementen van de verzameling.
Hier zijn enkele van de voorbeelden van functioneel volledige verzamelingen:
--> {En, of, niet}
--> {AND, NOT}
--> {Of, niet}
--> {NAND}
--> {Noch}
Het kiezen van een ontwerp voor een functioneel complete set maakt het werk een stuk makkelijker aangezien we gewoon een combinatie van de elementen maken het ontwerp voor de anderen kunnen trapsgewijs. In dit geval, ik koos voor de set: {of, niet}
De OR(+) poort en de OMVORMER (niet ~) het volgende kenmerk heeft, zoals weergegeven in de afbeelding (A en B zijn logische ingangen).
Hier is het implementeren van enkele van de andere logica poorten met behulp van de set {of, niet}:
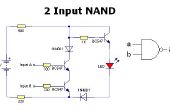
* Het implementeren van een NAND poort:
~(AB) = ~ A + ~ B
* Implementeren en poort:
AB = ~~(AB) = ~ (~ A + ~ B).
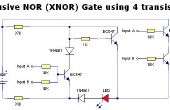
* Implementeren NOR poort:
~(A + B)