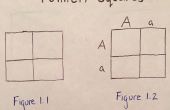
Stap 2: Berekening van kwadraten van getallen van 76 tot 125

Gebruik de volgende methode voor het berekenen van de kwadraten van getallen van 76 tot 125:
a) selecteert u een nummer 'x' variërend van 76 en 105.
Voorbeeld: x = 121
b) zoeken verschil van dit nummer van 100 d.w.z. y = + |x – 100|. Dit verschil zou liggen tussen -25 en 25.
Voorbeeld: y = (121 – 100) = 21
c) vinden plein van dit verschil. Y2 = (x-100) 2. Laatste twee cijfers van dit plein zouden vormen de eerste en tweede plaats cijfers van rechts op het definitieve plein. Elke derde cijfer van dit plein zou worden overgedragen naar de honderste plaats.
Voorbeeld: y2 = (21) 2 = 441
In het voorbeeld zou 41 de laatste twee cijfers van het laatste vierkant vormen terwijl 4 zou worden overgedragen naar het derde cijfer van rechts.
d) toevoegen het verschil met het nummer zelf dus z = x + y. Dit kan ook worden geschreven als z = (100 + 2y)
Enen en tientallen plaats cijfer van dit getal zal het derde en vierde cijfer van rechts van het laatste vierkant vormen. Elke derde cijfer van dit nummer zou worden overgedragen naar de vijfde plaats.
Voorbeeld: z = 121 + 21 = 142 of z = 100 + (2 * 21) = 142
42 zullen hier, de duizenden en nog eens honderden cijfers van het laatste vierkant vormen. 1 zal worden vervoerd naar voren als vijfde cijfer
e) brengen samen de eerste twee en de laatste twee cijfers van het laatste vierkant d.w.z. _z_ _y2_
Voorbeeld: 142 + 441 = 14641