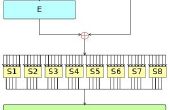
Stap 2: Niet-binaire, niet Bitsgewijze XOR

Dus de grote vraag is kan dit soort dingen werken met cijfers en niet alleen op binair niveau. Ik geloofde dat het kon dus ik heb geprobeerd om het uit te werken in mijn hoofd en op papier. Dit is wat ik dacht zou het resultaat voor base10.
Een xor B = C--> C xor B = A--> C xor A = B
0123456789--> 10 cijfers
10-9 = 1-3 =-2-3 > xor 9 = 8--> 8 xor 9 = 3
10-8 = 2-3 =-1--> 3 xor 8 = 9--> 9 xor 8 = 3
10-7 = 3-3 = 0--> 3 xor 7 = 0--> 0 xor 7 = 3
10-6 = 4-3 = 1 -> 3 xor 6 = 1--> 1 xor 6 = 3
10-5 = 5-3 = 2-3 > xor 5 = 2--> 2 xor 5 = 3
10-4 = 6-3 = 3--> 3 xor 4 = 3--> 3 xor 4 = 3
10-3 = 7-3 = 4 -> 3 xor 3 = 4 -> 4 xor 3 = 3
10-2 = 8-3 = 5--> 3 xor 2 = 5--> 5 xor 2 = 3
10-1 = 9-3 = 6--> 3 xor 1 = 6--> 6 xor 1 = 3
10-0 = 10-3 = 7--> 3 xor 0 = 7--> 7 xor 0 = 3
Natuurlijk werkt mijn wiskunde niet heel goed voor codering op de computer. In plaats daarvan moet het positionele gebaseerd met een set. De set is het alfabet dus-te-spreken. De lengte van het alfabet en de positie van de wedstrijden zijn de belangrijkste factoren voor de codering. Laten we eens kijken als we een binaire versie om de theorie te testen kunnen doen. Dus is het alfabet in binary, gemakkelijk "0" en "1".
Instellen "0" = "1"
Lengte = 2
Max = 1
A = 1, B = 1, C =?
Max - standpunt1 - postion2 = position3
1 - 2 - 2 = -3
Oh, oh! -3? Heb ik besloten dat de gemakkelijkste oplossing hiervoor is om te controleren voor een niet-positief geheel getal en herschrijven van de waarde zoals ik achteruit zonder "Carry-over" of de rest rekende.
In dit binaire voorbeeld kan er alleen worden twee posities "1" en "2".
Als ik de lengte van de verzameling, die 2 -3 is -1 bij toevoegen, toevoegen van lengte weer en we hebben 1. Op deze basis zou 0 -2 evalueren en naar positie 2.
Onder deze voorwaarden zal dit werken de waarheidstabel voor een Bitsgewijze XOR wordt geëmuleerd doordat:
A(in) POS(a) B(in) POS(b) C(out) POS(c)
0 1 0 1 0 1
1 2 0 1 1 2
0 1 1 2 1 2
1 2 1 2 0 1
.