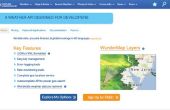
Stap 5: Hoe de lengte van de omtrek van een veelhoek gewijzigd wanneer het aantal zijden verdubbelt

Zullen we het overwegen van een getrokken binnen een cirkel met straal 1, zodat de lengte van OC, OA en OB lijnen veelhoek = 1.
Lijn OC snijdt lijn AB doormidden op punt X.
L de lengte van zijde AB van onze oorspronkelijke veelhoek en N worden de lengte van de AC kant nieuwe laat.
Dus de lengte van de lijn AX = L/2.
Voor het berekenen van N, kunnen we de stelling van Pythagoras op driehoek AXC gebruiken:
AC² = AX² + XC²
dus
N² = (L/2) ² + XC²
Om te zoeken naar XC, onthoud OC = 1 en OC = OX + XC, zo
XC = 1 - OX
Wat betekent
N²= (L/2)² + (1 - OX)² . . . . . . . . . Vergelijking 1
Merk op dat OX is deel een schuine driehoek OXA. We weten OA = 1 en XA = L/2, dus met behulp van Pythagoras op deze driehoek we vinden:
OA² = OX² + XA²
dat geeft
1² = OX² + (L/2) ²
dus OX² = 1 - (L/2) ²
We kunnen vervangen dit weer in vergelijking 1:
N² = (L/2) ² + (1 - OX) ² = (L/2) ² + (1 - √ (1 - (L/2) ²)) ²
wat vereenvoudigt om te
N = √(2 - 2 √(1 - (L/2)²))) . . . . . . . . . Vergelijking 2
We hebben nu een vergelijking die betrekking heeft op de lengte van de zijden L van een gegeven veelhoek binnen een cirkel met straal 1 met de lengte van de zijden N in een veelhoek met dubbele het aantal zijden zit in die dezelfde cirkel.