Stap 7: Geavanceerde schildpad gebaseerde tekening






Met behulp van de methoden datumwaarde, rechts(), up() en down() voor de schildpad is eenvoudig. Maar voor sommige tekeningen moeten we meer geavanceerde 3D controle. Bijvoorbeeld, zou u wilt tekenen een donut 45 graden omhoog gekanteld. Het is verleidelijk om het glas donut script uit de vorige stap, en toevoegen vóór de lus:
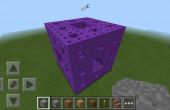
Maar dat levert een onverwacht resultaat--zie de foto. De reden hiervoor is dat de schildpad omhoog de hele tijd, klimmen zal terwijl de d.left()-methode draait het om de verticale as, en dus krijg je een spiraal.
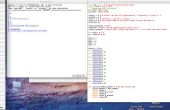
Wat we moeten doen is daarentegen yaw/pitch/roll rotatins de schildpad. Zie de foto van NASA (Amerikaanse regering werken zijn openbaar domein) uit te leggen hoe de drie hoeken gaan, en alleen maar denken dat het vliegtuig uw schildpad is. (Helaas wegens Minecraft beperkingen, de roll-hoek heeft geen invloed op de weergave van de schildpad of het oogpunt waaruit u bekijkt.) Wat we moeten doen om te tekenen onze zijwaarts donut is eerste worp onze schildpad 45 graden met t.roll(45), en vervolgens wanneer tekenen van de donut gebruik t.yaw(-angle) in plaats van t.left(angle). De herziene code is in de screenshot.
Wat is er leuk over de rotaties yaw/pitch/roll is dat ze altijd ten opzichte van waar de schildpad wijst, terwijl de datumwaarde en rechts() ten opzichte van de Minecraft wereld zijn.
Tot slot, hier is een veel meer geavanceerde voorbeeld. Laten we trekken een boom. Dit omvat het maken van een recursieve functie. Beginnen met dit om ervoor te zorgen dat de tekening zo snel mogelijk
Nu doen we onze recursieve boom functie. Het basisidee achter dit is dat een filiaal gewoon een kleinere boom is. Dus maken we een functie waarmee een teller en een lengte van de tak. De teller geeft aan hoeveel iteraties de boom zal gaan. Bijvoorbeeld, counter = 1 betekent gewoon de stam zal worden getrokken, en counter = 1 betekent dat de stam en één set takken zullen worden getrokken.
De code controleert eerst, als onze teller heeft reduceren tot nul. Zo ja, hebben we niets te tekenen. Dan tekenen we een kofferbak. Dan tekenen we vier takken steken eruit met een eenvoudige lus. Voor het ontwerpen van dit codefragment, ik kan me voorstellen mezelf als de schildpad, hebben net verhuisd omhoog langs de romp. Om te tekenen op een tak, ik mijn zelf omhoog kantelen door 30 graden (bijvoorbeeld t.pitch(30)) en tekenen van een nieuwe boom van kleinere omvang: de teller is minder door een, en de romp zal 3/4 van de lengte van mijn huidige koffer. Ik denk dat tilt mezelf terug naar beneden 30 graden. Ik mezelf 90 graden draaien en herhaal de oefening. Ten slotte, zodra ik klaar ben met de takken, ik ga terug naar beneden de kofferbak.
Tot slot, ik moet gewoon zich te beroepen op deze code. Ik wil een boom met een teller van 6 en een lengte van de eerste tak van 20. En voor een goede maatregel, I'l maken van hout, en uiteraard verticaal opwaartse:
Deze fractal boom ziet er niet erg realistisch. Moeten we de dikke stam en de takken dunner en dunner als ze naar buiten gaan krijgen (zeg, krijgen half zo dik, totdat ze één blok), en wij moeten overschakelen van hout naar verlaat blokken zoals wij uitgaan. Maar bovenal echte bomen zijn dat regelmatig niet. We moeten sommige willekeurigheid. De eenvoudigste vorm van willekeur is gewoon elke tak een kans te geven niet om te groeien, zeggen een 20% kans. Ik heb al deze in mijn fancytree.py scriptgeïmplementeerd. De resulterende boom kijkt verrassend realistische voor iets geproduceerd door zo'n relatief eenvoudig stukje code. Een grappig bijwerking van hoe ik het geïmplementeerd is dat er een 20% kans dat niets zal worden getrokken--d.w.z., de boom heeft een kans om te groeien, die ook realistisch is. En elke keer dat u het script start, krijg je iets anders.
Een andere nuttige functie van de schildpad tekening klasse is kunnend trekken niet alleen de lijnen maar de veelhoekige oppervlakken. Om dit te doen, gewoon doen t.startface(), uw oppervlak trekken en voer t.endface(). Zodra u in de modus van het gezicht, elke keer dat u een lijn tekent, tekent de code eigenlijk een driehoek: een hoekpunt is het punt dat de schildpad was toen t.startface() werd genoemd en de regel is de tegenoverliggende rand. Dit trekt een vijfhoek gekanteld op zijn kant door 45 graden: