Stap 5: Maak de gecodeerde wielen




Nu moet ik schrijven van de letters van het alfabet op elk wiel in willekeurige volgorde. Een methode om dit te doen is schrijven alle letters uit op een stuk papier. Voor elke letter kiest ik willekeurig, ik het Kruis af van de lijst. Ik beginnen elk wiel met de hub uit te steken naar rechts. Ik schrijf dan de letter A op een segment dat een Spaak heeft. Het woord wordt gevoerd door schrijf ik een uniek nummer. Mijn set is eigenlijk slechts 13 wielen breed; mijn wielen zijn genummerd 1-13. Als ik moest eigenlijk maken een 26 wielen cypher, zou ik waarschijnlijk letters van het alfabet gebruiken voor het identificeren van elk wiel (A-Z).
Maak een set wielen, met elk wiel met een unieke willekeurige volgorde van letters. Maak vervolgens een exact duplicaat van de wielen voor de tweede set.
Als je jezelf te creëren willekeurige sequenties niet vertrouwt? Probeer dit:
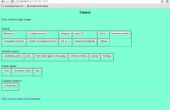
Open Microsoft Excel. Vul cellen A2 t/m A27 met het alfabet. (Cel A2 = 'A', A3 = 'B', A4 = 'C',...) Typ de letter A in cel B2. In cel B3, type in = INDEX ($A$ 2: $A$ 27, LARGE(MATCH(ROW($A$2:$A$27), ROW($A$2:$A$27)) * niet (aantal.als ($B$ 1: B2, $A$ 2: $A$ 27)), ASELECTTUSSEN (1, ROWS($A$2:$A$27)-ROW(A2)+1))). Maar, in plaats van op ENTER na het typen in de formule te drukken, drukt u op SHIFT + CTRL + ENTER. Dit zal tijdelijk zet {en} haakjes rond de formule. Nu cel B2 Kopieer en plak op cellen B3-B27. Hierdoor ontstaat een unieke lijst met letters waar elke letter is slechts éénmaal kan gebruiken. Dit verandert wanneer er een verandering in het werkblad, zoals het typen van de nummer 1 in cel C2.
Ik kopieer de gerandomiseerde letters en "Plakken speciaal - waarden" gebruiken om te plakken in verschillende kolommen te hebben een record van elk wiel.
Voor meer informatie over deze formule, ga naar deze link:
http://www.Get-Digital-Help.com/2009/07/03/How-to-...
HOEVEEL VERSCHILLENDE WIELEN ZIJN ER?
Laten we doen een beetje oefening om uit te vinden.
Laten we zeggen dat we hebben alleen 2 brieven. Aangezien dit op een wiel, kunnen we altijd draai het wieltje zodat de letter "A" ons uitgangspunt is. Als zodanig, is er slechts 1 mogelijke combinatie; NBA
3 letters: abc / acb - 2 combinaties
4 letters: abcd / abdc / acbd / acdb / adbc / adcb - 6 combinaties.
5 letters: abcde / abced / abdce / abdec / abecd / abedc / acbde / acbed / acdbe / acdeb / acebd / acedb / adbce / adbec / adcbe / adceb / adebc / adecb / aebcd / aebdc / aecbd / aecdb / aedbc / aedcb - 24 combinaties
Op basis van deze combinaties, het lijkt erop dat het aantal combinaties kan worden vertegenwoordigd door:
n = 2 brieven: (n-1) = (2-1) = 1 combinatie
n = 3 letters: (n-1)*(n-2) = (3-1)*(3-2) = 2 * 1 = 2 combinaties
n = 4 letters: (n-1)*(n-2)*(n-3) = 3 * 2 * 1 = 6 combinaties
n = 5 letters: (n-1)*(n-2)*(n-3)*(n-4) = 4 * 3 * 2 * 1 = 24 combinaties
Dit type berekening heet een faculteit en wordt vertegenwoordigd door een uitroepteken. IE 4! = 4 * 3 * 2 * 1
Dus, omdat er 26 letters van het alfabet. Opstijgen de letter A, omdat het is vastgesteld. Wij hebben 25! combinaties. Kunst
1.551121e + 25