Stap 4: Meer Math: berekenen van de lengtes van slingers
Tot nu toe hebben we de vereiste perioden die nodig zijn voor elke slinger. We hebben ook een vergelijking (van de vorige stap) die de periode als een functie van de constanten en twee variabelen, L en θ beschrijft:T=2*pi*sqrt(L/g)*K(θ).
Omdat ik wil bekijken mijn slinger-Golf vanaf de bovenkant, en moeten de amplitudes van elke golf die gelijk van die mening, heb ik verder de beperking:
L*sin(θ) = C
waar C is de constante amplitude voor alle golven.
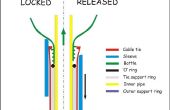
Hier is een cijfer aan te tonen deze eenvoudig concept:

Mijn methode voor het oplossen van de lengtes van de slingers was als volgt:
1) ben ik begonnen met slinger #18 in de serie (de slinger met de hoogste frequentie en de kortste lengte), het kiezen van een de waarde die ik voor de hoek van de max vrijlating van de hele reeks wilde. Ik koos voor pi/4 radialen of 45 graden. Alle andere release hoek zal kleiner is dan deze waarde worden.
2) ik deze waarde voor de release hoek aangesloten op de vergelijking van de slinger, dan L voor de vereiste periode opgelost.
3) met L en θ nu opgelost, berekend ik L*sin(θ) = constante.
4) voor de 17 slingers resterende, gebruikte ik Excel Oplosser-invoegtoepassing de periode vergelijking gelijk aan de vereiste periode instellen door het veranderen van de release hoek wanneer de lengte = C/sin(θ). Ik heb een afbeelding van dit proces verbonden. Voor meer informatie over Oplosser, Klik hier.