Unieke slinger Wave en Release mechanisme (5 / 10 stap)

Stap 5: Vrijgeven mechanisme Math - deel 1

Voor het behandelen van de timing voor elke release, laten we uitzoeken de geometrie eerst. We moeten de lengte van de arm van de release en de horizontale afstand tussen de release arm en de slinger bevestigingspunt vinden.

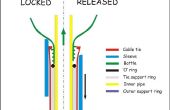
Het scenario voor slinger wordt afgebeeld in het diagram hieronder:

In de afbeelding

Lis de afstand van de slinger ondersteuning balk naar het midden van de slinger bob. Deze waarde staat bekend om elke slinger.

W is de horizontale afstand van de slinger bevestigingspunt naar het midden van de slinger bob bij release (L*sin(θ), iemand?).

R is de afstand van de arm bevestigingspunt aan de onderkant van de slinger bob. Deze waarde is zeer onbekend.

D is de afstand die ik wil de arm uit te breiden voorbij de bob wanneer de arm het verzamelt. Voor mijn slinger Golf koos ik 0,5".

S is de horizontale afstand van de slinger bevestigingspunt naar bevestigingspunt van de arm. Deze waarde is ook zeer onbekend.

C is de verticale afstand van het bevestigingspunt van de arm naar de onderkant van de slinger bob. Deze waarde wordt willekeurig geselecteerd (ik koos 4").

H is de verticale afstand van de bijlage van de arm naar de onderkant van de slinger bob bij release. Deze waarde is van inspectie, L-L * cos (θ) + C.

Oplossen voor de R- en S

We definiëren de arm door twee waarden: de lengte van de arm (R + D) en de vereiste offset (S). Laat oplossen voor deze waarden in termen van de drijvende (bekende) variabelen.

Om te beginnen, we weten dat de afstand W gelijk is het de som van S en de horizontale afstand tussen de S en de slinger release punt. Met behulp van de stelling van Pythagoras, kunnen we zeggen dat

W=SQRT(R^2-C^2)+SQRT((R+D)^2-H^2)

Kwadratuur van beide zijden van deze vergelijking en het isoleren van nul geeft de vierkantsvergelijking:

((W^2-R^2+C^2-(R+D)^2+H^2)^2)/4-(R^2-C^2)((R+D)^2-H^2)=0

Dit is een pijnlijke berekening op te lossen met de hand, dus ik suggereren met behulp van een programma zoals Matlab. Hier is hoe ik deze vergelijking in Matlab voor R: opgelost

>> syms R C H W D % definiëren variabelen
>> solve([W^2-R^2+C^2-(R+D)^2+H^2]^2/4-(R^2-C^2)*((R+D)^2-H^2),R) % oplossen voor R

ans =

(W * (C ^ 4-2 * C ^ 2 * D ^ 2-2 * C ^ 2 * H ^ 2 + 2 * C ^ 2 * W ^ 2 + D ^ 4-2 * D ^ 2 * H ^ 2-2 * D ^ 2 * W ^ 2 + H ^ 4 + 2 * H ^ 2 * W ^ 2 + W^4)^(1/2) - C ^ 2 * D + D * H ^ 2 + D * W ^ 2 - D ^ 3) / (2 * D ^ 2-2 * W ^ 2)

-(W * (C ^ 4-2 * C ^ 2 * D ^ 2-2 * C ^ 2 * H ^ 2 + 2 * C ^ 2 * W ^ 2 + D ^ 4-2 * D ^ 2 * H ^ 2-2 * D ^ 2 * W ^ 2 + H ^ 4 + 2 * H ^ 2 * W ^ 2 + W^4)^(1/2) + C ^ 2 * D - D * H ^ 2 - D * W ^ 2 + D ^ 3) / (2 * D ^ 2-2 * W ^ 2)

Merk op dat Matlab ons twee antwoorden geeft omdat we een kwadratisch opgelost. Welke oplossing we kiezen? Sluit in redelijke, positieve waarden in beide expressies om te beslissen, en zien welke oplossing geeft ons een redelijk en positief antwoord (de tweede vergelijking).

Dus,

R =-(W * (C ^ 4-2 * C ^ 2 * D ^ 2-2 * C ^ 2 * H ^ 2 + 2 * C ^ 2 * W ^ 2 + D ^ 4-2 * D ^ 2 * H ^ 2-2 * D ^ 2 * W ^ 2 + H ^ 4 + 2 * H ^ 2 * W ^ 2 + W^4)^(1/2) + C ^ 2 * D - D * H ^ 2 - D * W ^ 2 + D ^ 3) / (2 * D ^ 2-2 * W ^ 2).

D toevoegen aan deze waarde (zoals weergegeven in het diagram) geeft ons de diagonale lengte van de arm van het bevestigingspunt van de arm naar de onderkant van de slinger. Dit komt doordat de arm een rechthoek in plaats van een lijn worden zal.

Met R opgelost, kunnen we nu stelling van Pythagoras gebruiken om op te lossen voor S:

S = SQRT(R^2-C^2).

Eenvoudig genoeg.

Merk op dat de diagonale afstand van het centrum van de locatie van de pin arm naar de slinger op uitgave is R + D. De werkelijke lengte van de arm van de pin is

R_actual = SQRT((R+D)^2-t^2/4)

waar is t de breedte van de arm.