Stap 6: Release mechanisme Math - deel 2
Tot nu toe hebben we de dimensies die we moeten ervoor zorgen dat elke arm de slinger op de juiste locatie pakt en het op de juiste locatie brengt. Nu moeten we om ervoor te zorgen dat alle wapens release alle slingers op hetzelfde moment.Na het doen van een beetje schetsen, kwam ik met een eenvoudig mechanisme dat werkt. Dan de arm zijn er twee onderdelen in dit mechanisme. Als u wilt knoeien met de elektrotechnici, noem ik ze de rotor en de stator.

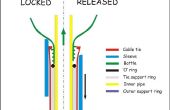
Als de afbeelding niet rechtvaardigheid doen, is hier een overzicht van hoe het ding werkt:
Elke arm (rood) heeft een sleuf gesneden van zijn kant. De rotor (groen) heeft twee stokjes, één aan elke kant, die uit te naar de "slots" van beide naburige wapens breiden. Het is aan de rug van twee stators (blauw) vastgemaakt. Alle rotoren zijn gekoppeld aan een deuvel op een constante afstand van de pin van de stator. Dus, wanneer een rotor beweegt, alle rotoren bewegen op de dezelfde hoeksnelheid. Met de juiste afmetingen voor de rotoren en stators (de arm afmetingen al zijn berekend), kunnen alle slingers tegelijkertijd worden gelost.
De instelling voor dit probleem is eenvoudiger dan het klinkt.
Oplossen voor z en Q

We moeten zoeken naar waarden van z en Q zodanig zijn dat bij een bepaalde hoek, Ï, het uiteinde van de arm een horizontale afstand L*sin(θ) van de slinger bevestigingspunt.
We hebben al S van het vorige probleem. J is een willekeurige waarde (het bepaalt de breedte van de slinger Golf frame).
R_c is een waarde die we voor later zal oplossen. Het is de afstand van de slinger release punt aan de lijn S. Het loopt parallel aan z.
U kunt dit probleem oplossen, zullen we gebruiken 3 vergelijkingen:
z/h = R_c/H
Q * sin (Ï) = h
J = Q * cos (Ï) + SQRT(z^2-h^2)
Wij lossen:
z/h = R_c/H = > h = z * H/R_c;
Q * sin (Ï) = h = > Q = z * H / (R_c * sin (Ï));
J = Q * cos (Ï) + SQRT(z^2-h^2) = > J = z * H * cos (Ï) / (R_c * sin (Ï)) + SQRT(z^2-(z*H/R_c)^2)
= > J = z * H * kinderbed (Ï) / R_c + z * SQRT(R_c^2-H^2)/R_c = > J = (z/R_c) * [H * kinderbed (Ï) + SQRT(R_c^2-H^2)]
= > z = J/(R_c*(SQRT(R_c^2-H^2) + H * kinderbed (Ï)))
En
Q = z * H / (R_c * sin (Ï))
Voor R_c op te lossen

R_c is de som van s (niet groot S uit de eerdere problemen) en de lengte van de rand van de arm (niet afgebeeld) beginnen bij de pin. Zoals vermeld op de vorige stap, is de werkelijke lengte van de arm anders dan de waarde R die we eerder berekend. Bovendien, is de hoek Ï anders dan de hoek die ï berekend net boven. Sorry voor de verwarring.
De werkelijke lengte, door Pythagoras, is:
R_actual = SQRT((R^2-t^2/4)
t is waar de dikte van de arm.
Dus,
R_c = R_actual + s.
We moeten om te vinden s, vindt u de waarde voor α, de hoek tegenover van s.
Uit het diagram, zien wij dat α = 180 - (Ï + 90 - β/2) = > α = 90 - Ï + β/2
waar Ï = asin(h/R) en β/2 = asin(t/(2*r)).
Ja, α = 90 - asin(h/R) + asin(t/(2*r)).
Tan(α) = 2 * s/t = > s = t * tan (α) / 2 = > s = t * tan(90-asin(h/R) + asin(t/(2*R)))/2
Dus,
R_c = SQRT(R^2-t^2/4) + t * tan(90-asin(h/R) + asin(t/(2*R)))/2
Voor mijn slinger Golf koos ik de release dikte (t) als 1/2".
We ontwierpen elke geleding in de release mechanisme te laten gaan van haar respectieve slinger, wanneer de rotor in een constante hoek (Ï is). Zo kan elke rotor gekoppeld worden aan alle andere rotoren. De implicatie hiervan is dat aangezien alle rotoren (wanneer die gekoppeld is) de zelfde hoeksnelheid hebben, en alle slingers zal worden gelost wanneer de rotor onder hoek Ï, alle slingers zal worden vrijgegeven op hetzelfde moment.