Stap 3: Onderscheiden!
![]()
![]()
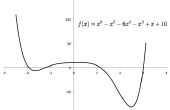
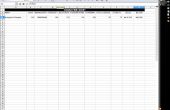
Uitzetten van de afgeleide is relatief eenvoudig. Een afgeleide heeft de vorm "dy/dx", met andere woorden, de wijziging in y over de wijziging in x. De wijziging in x is gemakkelijk, en verandert dit nooit meer, het is net wat we schreven in cel A2, die in dit geval is 0.1. De wijziging in y is gewoon gonna worden van het verschil tussen de cellen, die is niet moeilijk om erachter te komen. Typ in "=(C2-C1) / $een$ 2" voor cel D2, dan sleept u het naar beneden (of dubbelklik rechtsonder in de cel.) Het beeld moet geven u een goed idee van wat te doen. Er zal niet om het even wat in cel D1, door te differentiëren verliezen we een van de cellen, maar als uw dx klein genoeg is, het maakt niet uit. Zorg ervoor dat dit om in te typen in plaats van D1, D2 die manier wanneer u het helemaal naar beneden de laatste cel sleept weergeven niet een belachelijk groot getal
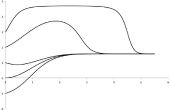
Plot dit op dezelfde grafiek als het laatste is, gebruik dezelfde x-waarden als vóór. Er is uw derivaat. U kunt ook met de hand doen van de afgeleide en plot om ervoor te zorgen dat deze overeenkomt met omhoog, het zou moeten.
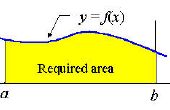
Dit is handig als u problemen ondervindt bij het differentiëren van een functie en u wilt zien hoe de afgeleide eruit. Zodra u de knie van differentiatie wel krijgen, het wordt vrij gemakkelijk en je gewoon echt nodig. Integratie aan de andere kant is vrij een beetje moeilijker, er zijn ook een aantal functies die je niet hoe weet te integreren. Laten we het doen met spreadsheets!